كيف تُساعدنا الرياضيات على فهم سرعة انتشار فيروس كورونا؟
عبر استخدام بضعة معادلات ومنحنيات رياضية بسيطة سنكون قادرين على فهم انتشار الفيروس ودور إجراءات الوقاية الصحية في كبح جماحه واحتوائه.

متى سيتوقف انتشار فيروس كورونا؟ ربما هذا هو السؤال الذي يشغل بال الكثيرين في الوقت الحاليّ عند الحديث عن الفيروس الذي تم اعتباره كوباءٍ عالميّ من قبل منظمة الصحة العالمية. تقوم الدول والحكومات بتسخير ما تمتلكه من طاقاتٍ وقدرات تقنية لاحتواء انتشار الفيروس الذي لا تزال كل الأرقام المرتبطة به سلبيةً بشكلٍ كبير حتى الآن، خصوصاً مع بعض التوقعات المتشائمة بأن يصيب الفيروس حوالي 60 – 70% من سكان الكوكب، وهذا ما أكدته المستشارة الألمانية أنجيلا ميركل بنفسها عندما صرّحت مؤخراً أن الفيروس قد يصيب أكثر من ثلثي سكان ألمانيا، أي حوالي 58 مليون نسمة.
من أين أتت هذه الأرقام؟ وكيف يستطيع البعض التنبؤ بأن فيروس كورونا قد ينتشر ليصيب ثلثي سكان الكوكب؟ قد يعتقد البعض أن الخروج بمثل هذه التوقعات يتم حتماً بالاعتماد على التقنيات الحديثة التي نستخدمها مثل برمجيات الذكاء الاصطناعيّ وتعلم الآلة، ولكن الحقيقة أنه بالعودة لمبادئ الرياضيات التي يدرسها طلاب المدارس الثانوية وطلاب السنوات الجامعية الأولى، سنستطيع تكوين صورةٍ جيدة عن كيفية انتشار الفيروس وما هي أسوأ – وأفضل الاحتمالات الممكنة التي تنتظرنا.
النمو الأسي: كيف تتزايد التجمعات السكانية؟
يقوم علماء الأحياء بدراسة كل شيء يعيش حولنا من نباتاتٍ وحيواناتٍ وحتى بكتيريا وفيروساتٍ صغيرة، ومن الأمور الأساسية التي يتوّجب فهمها كيفية انتشار التجمعات السكانية الخاصة بفصيلٍ حيّ، مثل الفيروسات. بمعنى آخر، يهتم علماء البيولوجيا دوماً بمعرفة كيفية سيتزايد أو يتناقص عدد الفيروسات ضمن بيئةٍ معينة ووفق شروطٍ معينة.
عند دراسة مثل هكذا تجمعات سكانية يتم عادةً اللجوء لمعادلةٍ رياضية بسيطة هي النمو الأسي Exponential Growth، وشكلها العمليّ وهو النمو اللوجستي Logistic Growth. تعبر كلا المعادلتين عن الكيفية التي سيتزايد بها عدد أفراد تجمعٍ سكانيّ، والفرق بينهما هو أن النمو الأسيّ يستمر إلا ما لا نهاية بينما يصف النمو اللوجستيّ تزايد عدد السكان حتى الوصول لقيمةٍ أو مرحلة لن يتزايد بعدها التعداد السكاني، وهي القيمة التي تُعرف بالإحصاء باسم سعة الحمل Carrying Capacity.
لفهم كيف يعمل النمو الأسيّ والنمو اللوجستي، لنعد للمثال الشهير المستخدم دوماً في حصص الرياضيات وحتى البيولوجيا: كيف سيتزايد عدد فصيلٍ من الأرانب خلال فترةٍ زمنية معينة؟ لو افترضنا أننا سنبدأ بمجموعةٍ من 10 أرانب، وأنه بكل يوم سيولد 5 أرانب جديدة وسيموت أرنبين، فهذا يعني أن معدل النمو Growth Rate هو الفارق بين عدد الأرانب الجديدة وعدد الأراتب المتوفاة مقسوماً على عدد الأرانب الأصلي، وبحالتنا هو 10، وهكذا سيكون معدل النمو هنا هو 0.3، وهكذا فإنه ومع كل يوم يمر، سيزادد عدد الأرانب بمقدار 30%، وهذا الأمر يُمكن توصيفه بمعادلةٍ رياضية بسيطة نستطيع عبرها التنبؤ بعدد الأرانب في يومٍ ما اعتماداً على معرفة معدل النمو وعدد الأرانب الأصلي:
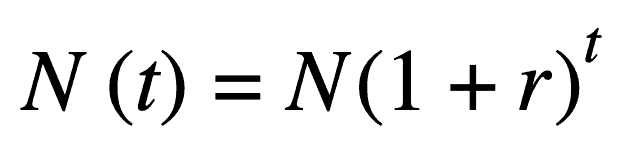
في المعادلة السابقة يمثل الحد (Nt) عدد الأرانب في اليوم (t) بينما يمثل الرمز r معدل النمو الخاص بالأرانب. كل شيء جيد حتى الآن باستثناء أمر وحيد: لو تركنا فصيل الأرانب هذا على حاله، فإنه وبحسب معادلة النمو الأسيّ السابقة ستتزايد أعداد الأرانب إلى ما لا نهاية، إذا ما بقي مُعدّل النمو الخاص بها ثابت وأكبر من الصفر، وهذا يختلف مع الواقع، حيث تؤثر العديد من العوامل في قدرة الأرانب على الانتشار والتكاثر: توّفر الغذاء، ووجود حيوانات أخرى تنافس الأرانب على مكان عيشها، وحتى نشاط البشر أنفسهم الذي أضر بأماكن الحياة الطبيعية للأرانب، وهكذا فإن معدل النمو لن يبقى على حاله بل سيبقى مُتزايداً حتى بلوغ نقطةٍ تُعرف باسم نقطة التحوّل Inflection Point والتي سيبدأ معها معدل النمو بالتناقص حتى وصول عدد الأرانب الكليّ لقيمةٍ ثابتة، أو سيتراوح حول قيمةٍ ثابتة تُدعى سعة الحمل Carrying Capacity. النمو اللوجستي هو التمثيل الأكثر واقعية لكيفية انتشار التجمعات السكانية كونه يأخذ بعين الاعتبار العوامل البيئية والتنافس على المصادر المتاحة والعوامل المضادة التي ستؤثر على معدل النمو وتجعله يتناقص. يمكن استخدام معادلة رياضية بسيطة لحساب النمو اللوجستي:
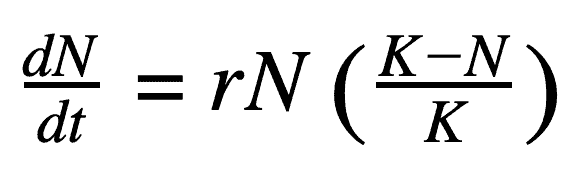
يُمثل الرمز K في المعادلة السابقة سعة الحمل، بينما يمثل الرمز N العدد الأولي للتجمع السكاني ويُمثل الرمز r معدل النمو، وأخيراً يمثل الحد dN/dt معدل الزيادة الحاصلة على عدد أفراد التجمع السكانيّ.
لا تستخدم معادلات ومنحنيات النمو الأسيّ واللوجستي لدراسة تكاثر وانتشار الأرانب فقط، بل تُطبق لفهم انتشار أي تجمعٍ سكانيّ للكائنات الحية، وانتشار البكتيريا والفيروسات ليس استثناءً لهذا الأمر.
فيروس كورونا والنمو الأسي
بالعودة لفيروس كورونا، ومع وصول عدد الإصابات لأكثر من 135 ألف إصابة ومع استمرار انتشار الفيروس منذ بداية العالم الحاليّ وحتى اليوم في جميع أنحاء الكوكب، أصبح هنالك كمية جيدة من البيانات التي يمكن استخدامها من أجل فهم سلوك الفيروس وكيفية انتشاره، ولو قمنا بتمثيل عدد الحالات المصابة بالفيروس مقارنةً مع الأيام، فإنه سنجد أن هنالك نمط نمو أسيّ يمكن ملاحظته باستخدام المنحني البياني التالي:
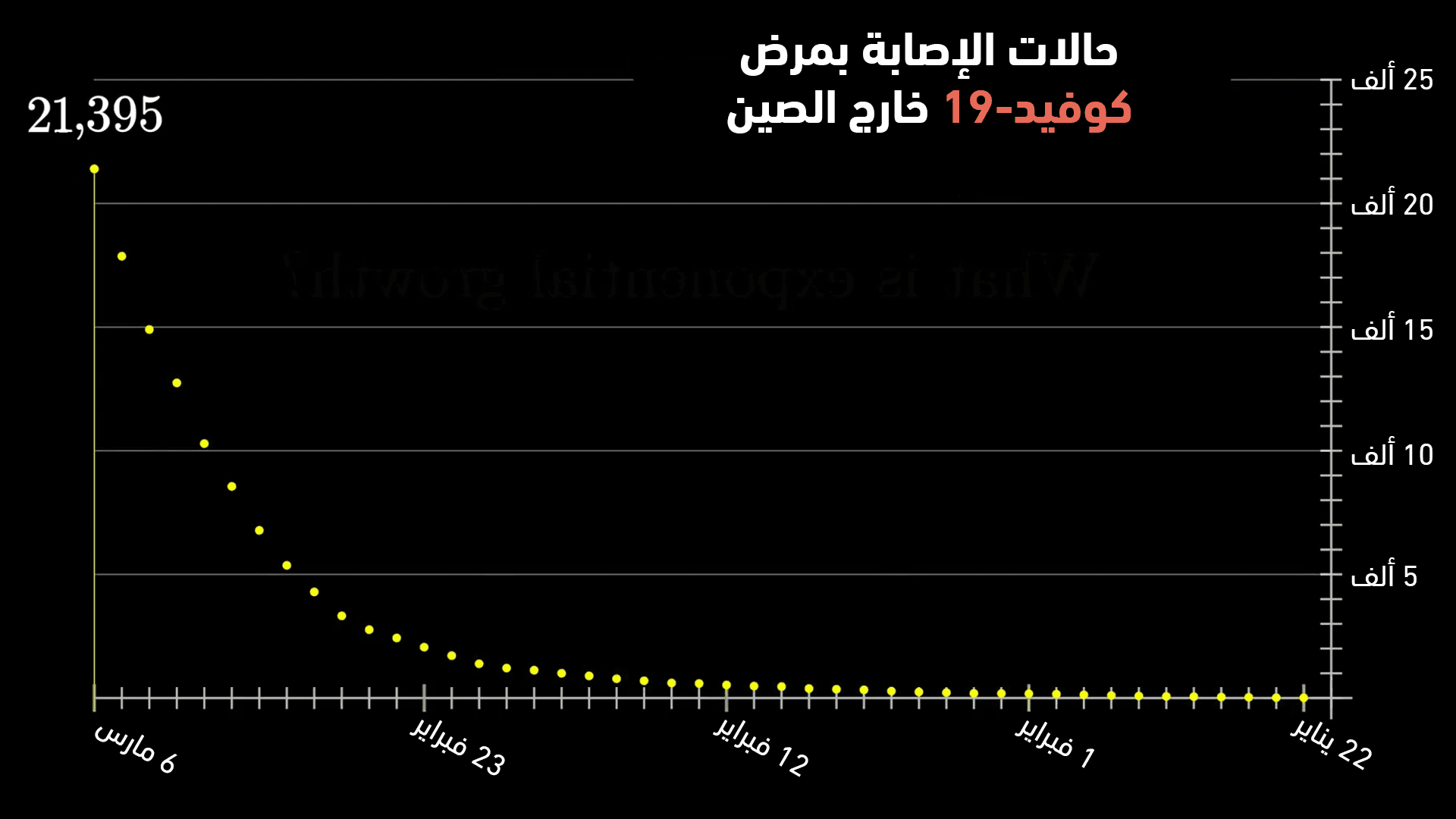
الصورة-1: تزايد عدد الإصابات بفيروس كورونا خارج الصين بدءاً من 22 يناير. حقوق ملكية الصورة: 3Blue1Brown
تم تعريبها من قبل إم آي تي تكنولوجي ريفيو
يمثل المنحنى السابق تزايد عدد الإصابات بالفيروس خارج الصين من الفترة الزمنية الممتدة من 22 يناير وحتى 6 مارس، ويمكن بشكلٍ سريع ملاحظة أنه وحتى تاريخ 23 فبراير كان هنالك تزايد بطيء بعدد الإصابات ومن ثم أصبح الإصابات بتزايدٍ أسيّ كبير، وهكذا فإنه يمكن استخدام معادلة النمو الأسيّ لفهم كيفية انتشار فيروس كورونا، وكذلك من أجل فهم عدد الإصابات المحتمل عند يومٍ محدد. لو عدنا لمعادلة النمو الأسيّ فإن ما يهمنا معرفته هو معدل النمو الخاص بالفيروس وما هي العوامل المرتبطة به والتي ستكون عاملين فقط – من باب التبسيط. هذه العوامل هي المعدل الوسطي للأشخاص الذين سيقابلهم شخص مصاب بالفيروس في كل يوم ولنسمي هذا العامل الرمز E، واحتمالية أن يؤدي كل تعرّض لحدوث إصابة، ولنسمي هذا العامل بالرمز p. وبالتالي ومن أجل توقع عدد الأشخاص المصابين بفيروس كورونا بيومٍ ما، يمكننا استخدام معادلة النمو الأسيّ كما يلي:
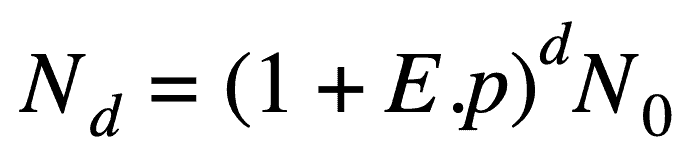
يمثل الرمز Nd عدد الأشخاص المصابين بفيروس كورونا في اليوم d، ويمثل الرمز N0 عدد الأشخاص المصابين بالفيروس عند بدء التوقع، وبهذه الحالة لنفترض أنه 6 مارس، وهذا يعني أن عدد الإصابات خارج الصين هو 21395 إصابة. أخيراً يمثل الجداء E.p معدل النمو، والذي سيتم اعتباره مساوياً للقيمة 1.15، وهي تساوي تقريباً قيمة معدل النمو الحقيقي الخاصة بالفيروس.
الآن لنفترض أن معدل النمو الحاليّ سيبقى على حاله، ولنحاول حساب عدد الإصابات المحتملة خارج الصين آخذين بعين الاعتبار 6 مارس كتاريخ للبداية، وعند استخدام معادلة النمو الأسيّ وإدخال كافة المعلومات المتوفرة حول الفيروس بهذا التاريخ، فإن أول ما سنلاحظه هو أن عدد الإصابات سيتزايد بمعدل 10 مرات كل 16 يوماً، وبالتالي وبدءاً من عدد إصابات بحدود 21 ألف إصابة بتاريخ 6 مارس، فإن عدد الإصابات الكليّ سيصل للمليون بعد 30 يوم، وسيصبح 10 مليون إصابة خلال 47 يوماً، وسيصبح 100 مليون خلال 64 يوماً وأخيراً سيصبح مليار إصابة خلال 81 يوماً، أي بتاريخ 26 مايو. الشكل التالي يظهر تزايد عدد الإصابات مع مرور الوقت ولكن بعد تحويله للتمثيل اللوغاريتمي:
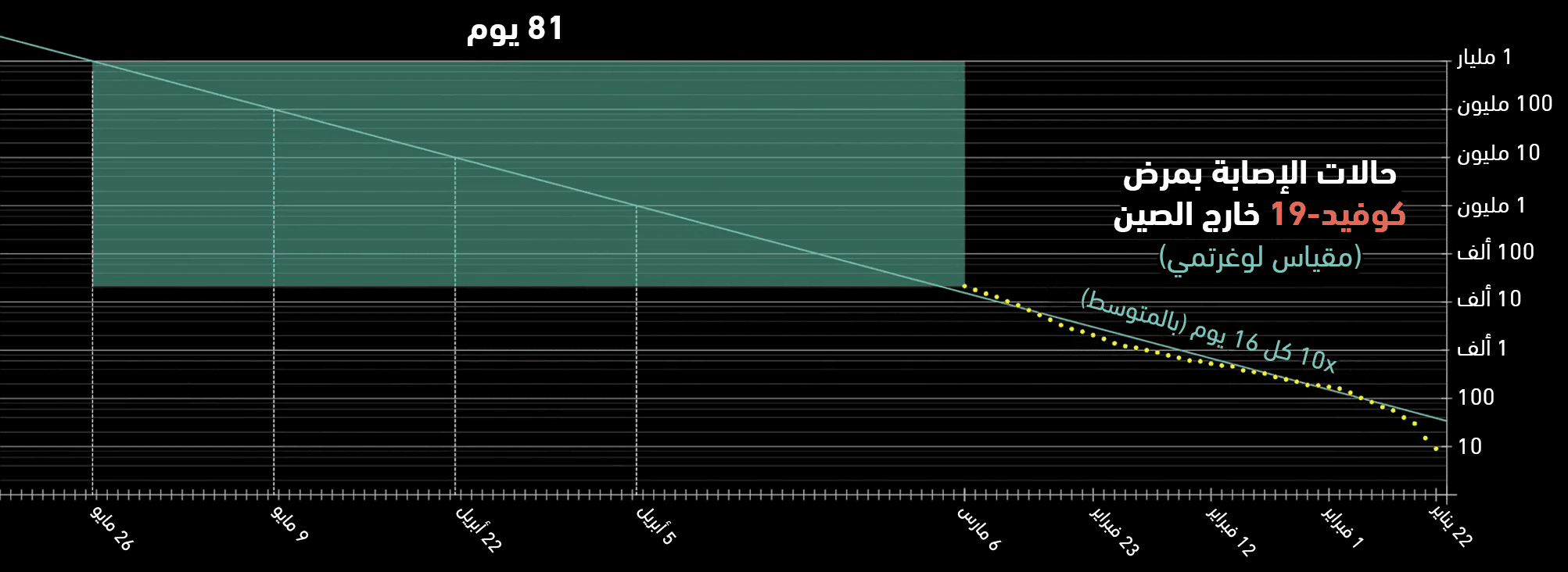
الصورة-2: قد يصل عدد الإصابات بالفيروس مليار شخص خارج الصين بحلول 26 مايو. حقوق ملكية الصورة: 3Blue1Brown
تم تعريبها من قبل إم آي تي تكنولوجي ريفيو
تعتبر الأرقام السابقة مفزعة إلى حدٍ ما، وهي تأخذ بعين الاعتبار بقاء معدل النمو على شكله الحالي، وإذا تزايد معدل النمو فإنها ستصبح أسوأ بكل تأكيد. لو أردنا الحديث بشكلٍ واقعيّ، فإن تزايد عدد الإصابات سيتبع على الأغلب نموذج النمو اللوجستي، أي أنه بيومٍ ما لن تتزايد أعداد الإصابات وستستقر عند قيمةٍ محددة. هذا الأمر يتبع لمعدل النمو، فطالما أنه ثابت أو متزايد ستزداد الإصابات بشكلٍ متواصل وبلا توقف، ولكن ومع تناقص معدل النمو وبلوغه قيمة 1.00، سيصل المنحني الخاص بتزايد معدل الإصابات القيمة المعروفة باسم نقطة التحول (Inflection Point) التي تمثل بدء مرحلةٍ جديدة يستمر معها معدل النمو بالتناقص حتى الوصول لقيمة الاستقرار المعروفة باسم سعة الحمل، والتي تشير إلى القيمة التي لن يتزايد بعدها عدد الإصابات. الشكل التالي يوضح تزايد عدد الإصابات تبعاً لنموذج المنحني اللوجستي:
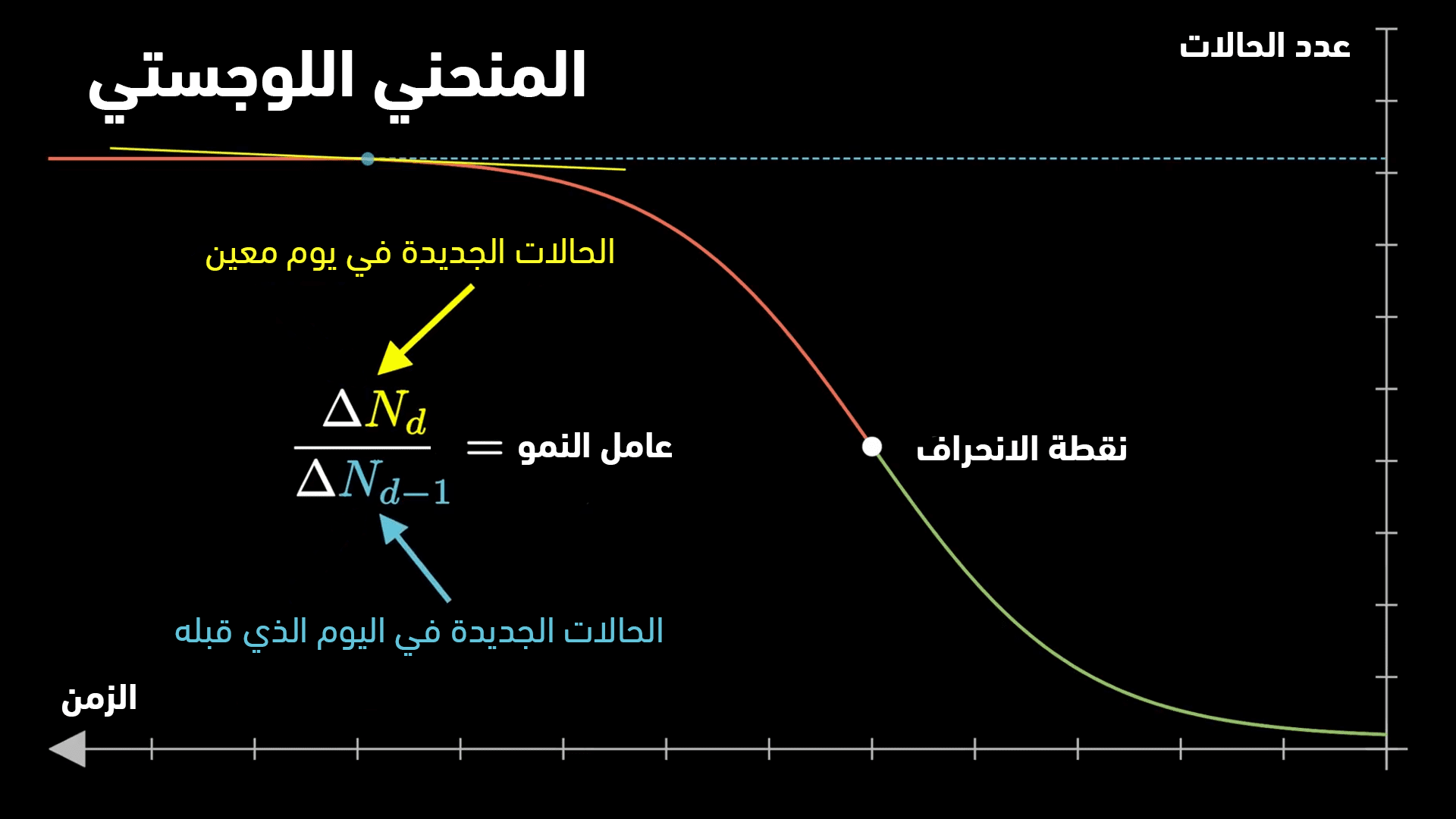
الصورة-3: المنحني اللوجستي الذي يظهر وصول عدد الإصابات لقيمةٍ مستقرة بعد تناقص معدل النمو. حقوق ملكية الصورة: 3Blue1Brown
تم تعريبها من قبل إم آي تي تكنولوجي ريفيو
متى سيحصل كل ذلك؟ أي متى سوف نصل إلى اللحظة التي لن تكون فيها إصابات جديدة ويتوقف الفيروس عن الانتشار ويتم احتوائه بشكلٍ كامل؟ لا أحد يعرف بشكلٍ دقيق، فهنالك العديد من العوامل التي تلعب دوراً بهذا الموضوع مثل الحرص على الالتزام بإجراءات الوقاية ومدى فعالية أنظمة الرعاية الصحية بالكشف عن الإصابات الجديدة وعزلها وحتى عبر مكافحة المعلومات الخاطئة المتعلقة بالفيروس وانتشاره وكيفية مكافحته، وهي عوامل من شأنها تخفيض معدل نمو الفيروس والحد من انتشاره كما أظهرت الإحصاءات القادمة من الصين والتي أكدت فعالية إجراءات حظر السفر في إبطاء حدة انتشار الوباء حول العالم، كما أن عدد الأشخاص الذين يشفون من الفيروس عاملٌ آخر هام يساهم بتخفيض معدل النمو لأنهم سيمثلون بتخفيض احتمالية الإصابات الجديدة. لتوضيح أثر تخفيض معدل النمو على زيادة عدد الإصابات، سنفترض أنه سيبقى عند قيمة 1.15، وعلى افتراض بدء الإحصاء من تاريخ 6 مارس عندما كان عدد الإصابات حوالي 21 ألف خارج الصين، فإنه من المتوقع بعد 61 يوماً أن يصل عدد الإصابات لحوالي 105 مليون شخص عند معدل نمو قدره 1.15. لو افترضنا الآن نجاح إجراءات الوقاية والتزام الأفراد بإرشادات الرعاية الصحية بما ساهم بتخفيض معدل النمو ليصبح 1.05، فإن عدد الإصابات بعد 61 يوماً سيكون حوالي 411 ألف إصابة.
تمثل الأرقام السابقة توقعاتٍ تقريبية ولا تأخذ كل العوامل المتعلقة بانتشار الفيروس بعين الاعتبار، كما أنها لا تأخذ نقطةً هامة تتعلق باحتمالية نشوء طفرة جديدة للفيروس قد تجعله قابلية العدوى به أعلى بما يعني ارتفاع معدل النمو الخاص به، ولكن معظم البيانات المتوفرة حتى الآن لا تشير لحدوث مثل هكذا أمر. بكل الأحوال، تشير الأرقام الأكيدة للحالات المسجلة أن شكل انتشاره يتبع بشكلٍ كبير لنموذج النمو اللوجستيّ والقدرة على التنبؤ بعدد الإصابات المستقبلية لا تزال ممكنة اعتماداً على معادلة النمو الأسيّ التي تم الإشارة لها في بداية المقال.
بهذه الصورة، وبالاستعانة بالرياضيات نستطيع فهم مدى تأثير سلوكنا كأفراد في الحد من الانتشار بالفيروس؛ الأمر يرتبط بشكلٍ أساسيّ بقدرتنا على تخفيض معدل النمو حتى الوصول لنقطةٍ مستقرة لا يتزايد بعدها عدد الإصابات، أي الاحتواء الكامل للفيروس. أسوأ التوقعات حالياً تشير إلى أننا قد نصل لهذه النقطة عندما يصبح ثلثي السكان مصابين بالفيروس، إلا أننا التطبيق الصارم لإجراءات الوقاية قد يعني أننا قد نصل لنقطة الاحتواء الكامل خلال وقتٍ أقصر.
